Quantum Numbers: H to Ne
There are four quantum numbers: n, ℓ, mℓ, and ms. Each one is a particular factor in an equation describing a property of the electron. At this introductory level, the equations are not needed. The value of each quantum number is assigned to each electron in an atom by a 'building up' process. Niels Bohr called this process the 'Aufbau' principle: aufbau means 'building up.'
n is ALWAYS the starting point for building up a series of quantum numbers. Each quantum number is then assigned according to a set of rules, each of which took years of study to finally determine. The rules ARE NOT just any old arbitrary ones; they have been determined from a study of nature. Remember the rules:
(principal quantum number n = 1, l = 0), because the pair of two electrons in the negative hydrogen ion replaces the one electron of the ordinary hydrogen. In the same way the ground state energy of the Helium atom with Z = 2 having two electrons is E = (-27.2)4 + (16.95) 2 - 4.1 = -79 eV which is the experimental value. The atomic number of each element increases by one, reading from left to right. Block Elements are organised into blocks by the orbital type in which the outer electrons are found. These blocks are named for the characteristic spectra they produce: sharp (s), principal (p), diffuse (d), and fundamental (f).

(1) n = 1, 2, 3, and so on.
(2) ℓ = 0, 1, 2, . . . , n - 1
(3) mℓ starts at negative ℓ, runs by whole numbers to zero and then goes to positive ℓ.
(4) after the n, ℓ and mℓ to be used have been determined, assign the ms value +½ to one electron, then assign the ms value of -½ to the next electron, while using the same n, ℓ and m values.
Also, keep in mind that we use only one n, ℓ, mℓ, and ms value each to make a set of four quantum numbers for each electron. It is this set of four quantum numbers that uniquely identifies each electron.
Last point: the last column in each table below is called 'Orbital Name.' As you are reading this tutorial, you may not yet know what an orbital is. That's OK, but please understand the concept called 'orbital' is an important one. Here's a real simple description that ignores lots of details: each orbital is a region of space around the nucleus which contains a MAXIMUM of two electrons. Realize that it's more complex than that, but the above description is good enough for now. I hope!!
Hydrogen - one electron
First Electron
n = 1
ℓ = 0
mℓ = 0
In each case, note that we start with the smallest value of n, ℓ, or mℓ possible. Make sure you look over the rules to see how each value was arrived at. ℓ starts at zero and goes to n - 1, which is zero since we get 1 - 1 = 0, when using n = 1. When ℓ = 0, there is only one possible choice for mℓ, which must be zero.
ms = +½
This completes the four quantum numbers for the single electron possessed by hydrogen. I shall build up a table like this:
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 1 | Hydrogen | 1 | 0 | 0 | +½ | 1s |
Helium - two electrons
First Electron
n = 1
ℓ = 0
mℓ = 0
ms = +½
The first electron in helium has exactly the same four quantum number of the first electron in hydrogen. However, helium has TWO electrons. So we 'build up' from the previous electrons by adding one more.
Second Electron
n = 1
ℓ = 0
mℓ = 0
ms = -½
Notice the same n, ℓ, and mℓ values, but ms has shifted from positive ½ to negative ½. This was the problem Pauli saw in 1925. Three quantum numbers was insufficient to UNIQUELY identify each electron, but a fourth one (the one called ms) did the trick.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 2 | Helium | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ |
Lithium - three electrons
The first two electrons quantum numbers' are EXACTLY the same as the two in helium:
1, 0, 0, +½ and 1, 0, 0, -½
Third Electron: here's where we 'build up' by adding one more electron.
However, we are now presented with a problem. All the values with n = 1 have been used up, but we have only accounted for two of lithium's three electrons. What to do about the third?
Answer: start with the NEXT n value; n = 2. However, there is a problem with ℓ; do we use ℓ = 0 or ℓ = 1, since both are possible with n = 2?
Answer: start with the lowest value first, so that means using ℓ = 0. (Don't worry, we will use ℓ = 1 soon enough.)
Figuring out mℓ should be easy; when ℓ = 0, mℓ can only equal 0. So n, ℓ, mℓ for the third electron is 2, 0, 0. I'll add in ms in the table below.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 3 | Lithium | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s |
Beryllium - four electrons
In the building up process, we go one electron at a time. Therefore, we will use the three from lithium and add one more.
Fourth Electron
n = 2
ℓ = 0
mℓ = 0
ms = -½
Notice the same n, ℓ, and m values as the third electron, but ms for the fourth electron has shifted from positive ½ to negative ½.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 4 | Beryllium | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ |
Pretty easy, eh? It stays easy, if you follow the rules. With beryllium, we have exhausted the possibilities for the n = 2; ℓ = 0 combination. However, when n = 2, ℓ can take on another value, namely ℓ = 1. This has consequences for the mℓ value as well and, after we finish, there will be six electrons that have a combination of n = 2 and ℓ = 1.
Here's the rule for mℓ again: start at negative ℓ, run by whole numbers to zero and then go to positive ℓ. Since ℓ = 1, we start with -1, go to zero and end up at +1. This gives us three values for mℓ when ℓ = 1. Hopefully you can see that, since ms takes on +½ and -½, we will wind up with six sets of quantum numbers.
Warning: there's going to be a new rule introduced after boron. So prepare yourself because, just as you thought it was getting easy, there gets added some new stuff. By the way, us mean old teachers didn't make all this stuff up to torture poor chemistry students. Nature really does do what I will explain below. Here's boron:
Boron - five electrons
Following the usual pattern, I've repeated the previous four electrons. As we go on to the ℓ = 1 values, keep in mind that we will start with the lowest value of mℓ, namely negative one.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 5 | Boron | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px |
Eventually, I will wind up with three orbital names. 2px is just the first, x meaning the x-axis. Next will be 2py, for the y-axis and the last name used will be 2pz, for the z-axis. These three orbitals are oriented at 90° to each other.
Hund's Rule (named for Fredrich Hund) is the name of the new rule. This rule concerns the relationship between the ℓ and mℓ quantum numbers. When ℓ = 0, mℓ can only equal zero and Hund's Rule does not show up. However, now that we have reached ℓ = 1, mℓ can take on multiple values. Hund's Rule concerns the order in which we assign the ℓ and mℓ values.
By the way, I'm going to avoid a technical statement of Hund's Rule for the moment. I'll discuss how it works first.
Hund's Rule means that we will use each possible ℓ, mℓ combination ONCE before going back and using it a second time. Here are the three possible ℓ, mℓ combos when ℓ = 1:
| ℓ | mℓ |
| 1 | -1 |
| 1 | 0 |
| 1 | +1 |
For boron, we have used the ℓ, mℓ combination of 1, -1. The key is to see that Hund's Rule requires we go on to the NEXT ℓ, mℓ combination for the next element: carbon.
Carbon - six electrons
Following the usual pattern, I've repeated the previous five electrons. As we continue on with the ℓ = 1 values, keep in mind that Hund's Rule will affect how we assign the next mℓ value.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 6 | Carbon | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| 2 | 1 | 0 | +½ | 2py |
Nitrogen - seven electrons
Since we still have not first used all possible ℓ, mℓ values ONCE, we go on to the next ℓ, mℓ combination.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 7 | Nitrogen | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| 2 | 1 | 0 | +½ | 2py | ||
| 2 | 1 | +1 | +½ | 2pz |
2px, 2py and 2pz are three different orbitals, each one capable of holding two electrons. Notice how, in nitrogen, each of the three orbitals is filled up HALF-WAY (that is, with one electron) before we go back and fill up each orbital with the second electron.
This 'half-filled orbital' has definite chemical consequences. Remember it well. Also, using 2px first, then going to y and then z is purely convention. The x, y, z order is not of consequence in the above examples. However keep in mind the using each letter ONCE first being using it for the second electron is important.
Oxygen - eight electrons
Now that we have used each ℓ, mℓ combination once, we proceed to go back and use each combo the second time. For oxygen to neon, I've marked which electron is the one added.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 8 | Oxygen | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| this one added | ---> | 2 | 1 | -1 | -½ | |
| 2 | 1 | 0 | +½ | 2py | ||
| 2 | 1 | +1 | +½ | 2pz |
Fluorine - nine electrons
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 9 | Fluorine | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| 2 | 1 | -1 | -½ | |||
| 2 | 1 | 0 | +½ | 2py | ||
| this one added | ---> | 2 | 1 | 0 | -½ | |
| 2 | 1 | +1 | +½ | 2pz |
Neon - ten electrons
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 10 | Neon | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| 2 | 1 | -1 | -½ | |||
| 2 | 1 | 0 | +½ | 2py | ||
| 2 | 1 | 0 | -½ | |||
| 2 | 1 | +1 | +½ | 2pz | ||
| this one added | ---> | 2 | 1 | +1 | -½ |
We have now completed all possible values for n = 1 AND n = 2. Starting with element 11, sodium, we will proceed on to n = 3. When we finish, we will have used ℓ = 0, ℓ = 1 (and applied Hund's Rule again) and then, before going on to ℓ = 3, we will hit another interesting twist that nature has handed us. We will wind up going on to n = 4 and then coming back to finish n = 3. It will be fun!
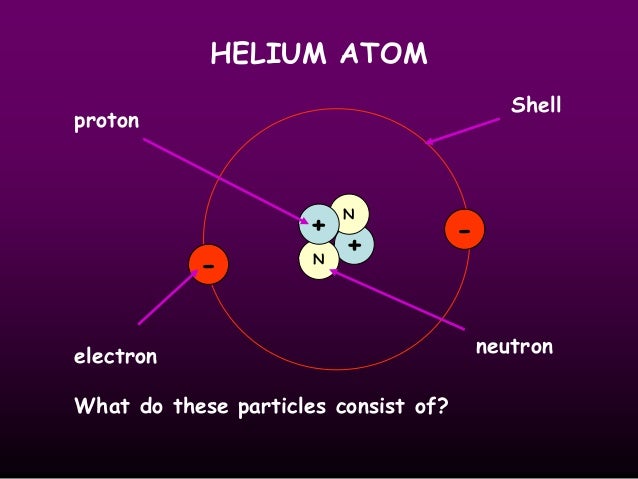
A typical atom consists of three subatomic particles: protons, neutrons, and electrons (as seen in the helium atom below). Other particles exist as well, such as alpha and beta particles (which are discussed below). The Bohr model shows the three basic subatomic particles in a simple manner. Most of an atom's mass is in the nucleus—a small, dense area at the center of every atom, composed of nucleons. Nucleons include protons and neutrons. All the positive charge of an atom is contained in the nucleus, and originates from the protons. Neutrons are neutrally-charged. Electrons, which are negatively-charged, are located outside of the nucleus.
Introduction
The Bohr model is outdated, but it depicts the three basic subatomic particles in a comprehensible way. Electron clouds are more accurate representations of where electrons are found. Darker areas represent where the electrons are more likely to be found, and lighter areas represent where they are less likely to be found.
| Particle | Electric Charge (C) | Atomic Charge | Mass (g) | Atomic Mass (Au) | Spin |
|---|---|---|---|---|---|
| Protons | +1.6022 x 10-19 | +1 | 1.6726 x 10-24 | 1.0073 | 1/2 |
| Neutrons | 0 | 0 | 1.6740 x 10-24 | 1.0078 | 1/2 |
| Electrons | -1.6022 x 10-19 | -1 | 9.1094 x 10-28 | 0.00054858 | 1/2 |
- Au is the SI symbol for atomic mass unit.
- The positive charge of protons cancels the negative charge of the electrons. Neutrons have no charge.
- With regard to mass, protons and neutrons are very similar, and have a much greater mass than electrons. Compared with neutrons and protons, the mass of an electron is usually negligible.
- Spin is associated with the rotation of a particle. Protons, neutrons, and electrons each have a total spin of 1/2.
Protons
Protons were discovered by Ernest Rutherford in the year 1919, when he performed his gold foil experiment. He projected alpha particles (helium nuclei) at gold foil, and the positive alpha particles were deflected. He concluded that protons exist in a nucleus and have a positive nuclear charge. The atomic number or proton number is the number of protons present in an atom. The atomic number determines an element (e.g., the element of atomic number 6 is carbon).
Electrons
Electrons were discovered by Sir John Joseph Thomson in 1897. After many experiments involving cathode rays, J.J. Thomson demonstrated the ratio of mass to electric charge of cathode rays. He confirmed that cathode rays are fundamental particles that are negatively-charged; these cathode rays became known as electrons. Robert Millikan, through oil drop experiments, found the value of the electronic charge.
Electrons are located in an electron cloud, which is the area surrounding the nucleus of the atom. There is usually a higher probability of finding an electron closer to to the nucleus of an atom. Electrons can abbreviated as e-. Electrons have a negative charge that is equal in magnitude to the positive charge of the protons. However, their mass is considerably less than that of a proton or neutron (and as such is usually considered insignificant). Unequal amounts of protons and electrons create ions: positive cations or negative anions.
Neutrons
Neutrons were discovered by James Chadwick in 1932, when he demonstrated that penetrating radiation incorporated beams of neutral particles. Neutrons are located in the nucleus with the protons. Along with protons, they make up almost all of the mass of the atom. The number of neutrons is called the neutron number and can be found by subtracting the proton number from the atomic mass number. The neutrons in an element determine the isotope of an atom, and often its stability. The number of neutrons is not necessarily equal to the number of protons.
Identification
Both of the following are appropriate ways of representing the composition of a particular atom:
Often the proton number is not indicated because the elemental symbol conveys the same information.
Consider a neutral atom of carbon: (ce{^{12}_{6}C}). The atomic mass number of Carbon is 12 amu, the proton number is 6, and it has no charge. In neutral atoms, the charge is omitted.
Above is the atomic symbol for helium from the periodic table, with the atomic number, elemental symbol, and mass indicated.
Every element has a specific number of protons, so the proton number is not always written (as in the second method above).
- # Neutrons = Atomic Mass Number - Proton Number
- Atomic mass number is abbreviated as A.
- Proton number(or atomic number) is abbreviated Z.
- # Protons = Proton Number or Atomic Number
- In neutral atoms, # Electrons = # Protons
- In ions, # Electrons = # Protons - (Charge)
- Charge is written with the number before the positive or negative sign
- Example, 1+
Note: The atomic mass number is not the same as the atomic mass seen on the periodic table. Click here for more information.
Other Basic Atomic Particles
Many of these particles (explained in detail below) are emitted through radioactive decay. Click here for more information. Also note that many forms of radioactive decay emit gamma rays, which are not particles.
Alpha Particles
Alpha particles can be denoted by He2+,α2+, or just α. They are helium nuclei, which consist of two protons and two neutrons. The net spin on an alpha particle is zero. They result from large, unstable atoms through a process called alpha decay. Alpha decay is the process by which an atom emits an alpha particle, thereby becoming a new element. This only occurs in elements with large, radioactive nuclei. The smallest noted element that emits alpha particles is element 52, tellurium. Alpha particles are generally not harmful. They can be easily stopped by a single sheet of paper or by one's skin. However, they can cause considerable damage to the insides of one's body. Alpha decay is used as a safe power source for radioisotope generators used in artificial heart pacemakers and space probes.
Beta Particles
Beta particles (β) are either free electrons or positrons with high energy and high speed; they are emitted in a process called beta decay. Positrons have the exact same mass as an electron, but are positively-charged. There are two forms of beta decay: the emission of electrons, and the emission of positrons. Beta particles, which are 100 times more penetrating than alpha particles, can be stopped by household items like wood or an aluminum plate or sheet. Beta particles have the ability to penetrate living matter and can sometimes alter the structure of molecules they strike. The alteration usually is considered damage, and can cause cancer and death. In contrast to beta particle's harmful effects, they can also be used in radiation to treat cancer.
Beta- (β-) or Electron Emission
Electron emission may result when excess neutrons make the nucleus of an atom unstable. As a result, one of the neutrons decays into a proton, an electron, and an anti-neutrino. The proton remains in the nucleus, and the electron and anti-neutrino are emitted. The electron is called a beta particle. The equation for this process is given below:
[ _{1}^{0}textrm{n}rightarrow {_{1}^{1}textrm{p}}^+ + textrm{e}^- + bar{nu_{e}} ]
- n = Neutron
- p+ = Proton
- e- = Electron (beta particle)
- νe = Anti-neutrino
β- Decay
Beta+(β+)or Positron Emission
Position emission occurs when an excess of protons makes the atom unstable. In this process, a proton is converted into a neutron, a positron, and a neutrino. While the neutron remains in the nucleus, the positron and the neutrino are emitted. The positron can be called a beta particle in this instance. The equation for this process is given below:
[ { _{1}^{1}textrm{p}}^+ rightarrow _{1}^{0}textrm{n} + textrm{e}^+ + nu_{e} ]
- n = Neutron
- p+ = Proton
- e+ = Positron (beta particle)
- νe= Neutrino
β+ Decay
Outside Links
- Basic Sub-Atomic Particles: www.youtube.com/watch?v=lP57g...eature=related
- Alpha Particles: en.Wikipedia.org/wiki/Alpha_decay
- Beta Particles: en.Wikipedia.org/wiki/Beta_particle
- What are Sub-Atomic Particles?: www.youtube.com/watch?v=uXcOqjCQzh8
- Atomic Number and Mass Number: www.youtube.com/watch?v=lDo78hPTlgk
References
- Petrucci, Ralph, William Harwood, Geoffrey Herring, and Jeffry Madura.General Chemistry. 9th ed. Upper Saddle River, New Jersey: Pearson Prentince Hall, 2007.
- Haskin, Larry A. The Atomic Nucleus and Chemistry; D. C. Heath and Company: Lexington, MA, 1972; pp. 3-4, 43-53.
- Petrucci, Ralph, F. Geoffrey Herring, Jeffrey D. Madura, and Carey Bissonnette. General Chemistry. 10th ed. Upper Saddle River, New Jersey: Pearson Education, Inc., 2011.
Helium Number Of Protons And Electrons
Problems
1. Identify the number of protons, electrons, and neutrons in the following atom.
2. Identify the subatomic particles (protons, electrons, neutrons, and positrons) present in the following:
- (ce{^{14}_6C})
- (alpha)
- (ce{^{35}Cl^-})
- (beta^+)
- (beta^-)
- (ce{^{24}Mg^{2+}})
- (ce{^{60}Co})
- (ce{^3H})
- (ce{^{40}Ar})
- (^1_0n)
3. Given the following, identify the subatomic particles present. (The periodic table is required to solve these problems)
- Charge +1, 3 protons, mass number 6.
- Charge -2, 7 neutrons, mass number 17.
- 26 protons, 20 neutrons.
- 28 protons, mass number 62.
- 5 electrons, mass number 10.
- Charge -1, 18 electrons, mass number 36.
4. Arrange the following elements in order of increasing (a) number of protons; (b) number of neutrons; (c) mass.
27Co, when A=59; 56Fe, when Z=26; 11Na, when A=23; 80Br, when Z=35; 29Cu, when A=30; 55Mn, when Z=25
5. Fill in the rest of the table:
| Atomic Number | Mass Number | Number of Protons | Number of Neutrons | Number of Electrons |
|---|---|---|---|---|
| 2 | 2 | |||
| 23 | 11 | |||
| 15 | 16 | |||
| 85 | 37 | |||
| 53 | 74 |
Solutions and Explanations
1. There are 4 protons, 5 neutrons, and 4 electrons. This is a neutral beryllium atom.
2. Identify the subatomic particles present in the following:
- 146C
- 6 protons, 8 neutrons, 6 electrons
- There are 6 protons in accordance with the proton number in the subscript. There are 6 electrons because the atom is neutral. There are 8 neutrons because 14-6=8. 14 is the atomic mass number in the superscript.
- 6 protons, 8 neutrons, 6 electrons
- α
- 2 protons, 2 neutrons, 0 electrons
- This is an alpha particle which can also be written as 4He2+. There are two protons because the element is helium. There are no electrons because 2-2 = 0. There are 2 neutrons because 4-2=2.
- 2 protons, 2 neutrons, 0 electrons
- 35Cl-
- 17 protons, 18 neutrons, 18 electrons
- This is a chloride ion. According to the periodic table, there are 17 protons because the element is chlorine. There are 18 electrons due to the negative charge: 17-(-1) = 18. There are 18 neutrons because 35-17=18.
- 17 protons, 18 neutrons, 18 electrons
- β+
- 0 protons, 0 neutrons, 0 electrons, 1 positron
- This is a beta+ particle. It can also be written as e+. 'e' represents an electron, but when it has as positive charge it is a positron.
- 0 protons, 0 neutrons, 0 electrons, 1 positron
- β-
- 0 protons, 0 neutrons, 1 electron
- This is a beta- particle, and can also be written as e-. This is a standard electron.
- 0 protons, 0 neutrons, 1 electron
- 24Mg2+
- 12 protons, 12 neutrons, 10 electrons
- This is a magnesium Ion. There are 12 protons from the magnesium atom. There are 10 electrons because 12-2 = 10. There are 12 neutrons because 24-12 = 12.
- 12 protons, 12 neutrons, 10 electrons
- >60Co
- 27 protons, 33 neutrons, 27 electrons
- The cobalt atom has 27 protons as seen in the periodic table. There are also 27 electrons because the charge is 0. There are 33 neutrons because 60-27 = 33.
- 27 protons, 33 neutrons, 27 electrons
- 3H
- 1 protons, 2 neutrons, 1 electrons
- There is 1 proton because the element is hydrogen. There is 1 electron because the atom is neutral. There are 2 neutrons because 3-1 = 2.
- 1 protons, 2 neutrons, 1 electrons
- 40Ar
- 18 protons, 22 neutrons, 18 electrons
- There are 18 protons from the argon element. There 18 electrons because it is neutral, and 22 neutrons because 40 - 18 = 22.
- 18 protons, 22 neutrons, 18 electrons
- n
- 0 protons, 1 neutrons, 0 electrons
- This is a free neutron denoted by the lower case n.
- 0 protons, 1 neutrons, 0 electrons
3. Given the following, identify the subatomic particles present. (The periodic table is required to solve these problems)
- Charge +1, 3 protons, mass number 6.
- 3 protons, 3 neutrons, 2 electrons
- Charge -2, 8 neutrons, mass number 17.
- 9 protons, 8 neutrons, 7 electrons
- 26 protons, 20 neutrons.
- 26 protons, 20 neutrons, 26 electrons
- 28 protons, mass number 62.
- 28 protons, 34 neutrons, 28 electrons
- 5 electrons, mass number 10.
- 5 protons, 5 neutrons, 5 electrons
- Charge -1, 18 electrons, mass number 36.
- 17 protons, 19 neutrons, 18 electrons
4. Arrange the following lements in order of increasing (a) number of protons; (b) number of neutrons; (c) atomic mass.
a) Na, Mn, Fe, Co, Cu, Br
- Z=#protons;
- Na: z=11; Mn: Z=25, given; Fe: Z=26, given; Co: Z=27; Cu: Z=29; Br: Z=35, given
b) Na, Cu, Fe, Mn, Co, Br
- A=#protons+#neutrons, so #n=A-#protons(Z);
- Na: #n=23-11=12; Cu: #n=59-29=30; Fe: #n=56-26=30; Mn: #n=55-25=30; Co: #n=59-27=32; Br: #n=80-35=45
Note: Cu, Fe, Mn are all equal in their number of neutrons, which is 30.
c) Na, Mn, Fe, Co, Cu, Br
- Na: 22.9898 amu; Mn: 54.9380 amu; Fe: 55.845 amu; Co: 58.9332 amu; Cu: 63.546 amu; Br: 79.904
Note: This is the same order as the number of protons, because as Atomic Number(Z) increases so does Atomic Mass.
5. Fill in the rest of the table:
| Atomic Number | Mass Number | Number of Protons | Number of Neutrons | Number of Electrons |
|---|---|---|---|---|
| 2 | 4 | 2 | 2 | 2 |
| 11 | 23 | 11 | 12 | 11 |
| 15 | 31 | 15 | 16 | 15 |
| 37 | 85 | 37 | 48 | 37 |
| 53 | 127 | 53 | 74 | 53 |
Note: Atomic Number=Number of Protons=Number of Electrons and Mass Number=Number of Protons+Number of Neutrons
Contributors and Attributions
Helium-4 Number Of Electrons
- Jiaxu (Josh) Wang (UCD)
